Splay学习笔记

Author Avatar
Sophon 3月 28, 2019
| keyboard本文共:1.7k字 | query_builder阅读时间≈7分 |
  • 在其它设备中阅读本文章

前言

伸展树（英语：Splay Tree）是一种能够自我平衡的二叉查找树，它能在均摊O(log n)的时间内完成基于伸展（Splay）操作的插入、查找、修改和删除操作。

众所周知，普通BST在进行各种操作时很容易因为左子树与右子树高度差的问题导致时间复杂度退化为O(n)，Splay为了避免这个问题，使用了一种叫做“伸展”的操作来使左右子树平衡，在后面会介绍。

定义

节点

node.v：节点node的值

node.father：节点node的父节点

node.ch[0]与node.ch[1]：节点node的左子节点与右子节点

node.size：以节点node为根节点的子树的节点总数

node.cnt：数值与节点node相同的节点的数量（都储存在节点node中）

代码：

class Node {
public:
    int v, father, ch[2], size, cnt;

    Node(int v = 0, int father = 0, int size = 0, int cnt = 0):v(v), father(father), size(size), cnt(cnt) {
        ch[0] = ch[1] = 0;
    }
};

树

root：根节点

cnt：总结点数

Node node[MAXN];
int root = 0, cnt = 0;

操作

基本操作

pushup

pushup()函数：更新节点p的size值

void pushup(int p) {
    node[p].size = node[node[p].ch[0]].size + node[p].cnt + node[node[p].ch[1]].size; //节点数 = 左子树节点数 + 本身的节点数 + 右子树节点数
}

check

check()函数：询问节点p是其父节点的左子节点还是右子节点

int check(int p) {
    return node[node[p].father].ch[0] == p ? 0 : 1; //0代表左子节点，1代表右子节点
}

connect

connect()函数：将节点x连接为节点f的子节点，方向为d (d = 0, 1，同上)

void connect(int x, int f, int d) {
    node[f].ch[d] = x; //将节点f的子节点设置为x
    node[x].father = f; //将节点x的父节点设置为f
}

旋转

rotate

旋转是平衡树最主要的操作，其本质在于，每次进行旋转时，左右子树当中之一高度 -1，另外一棵高度 +1，以达到平衡的目的。

左旋：

第一次连边，节点x的子节点成为x的父节点的右子节点

第二次连边，节点x成为节点x的父节点的父节点的子节点，方向与x的父节点相同

第三次连边，节点x的父节点成为节点x的左子节点

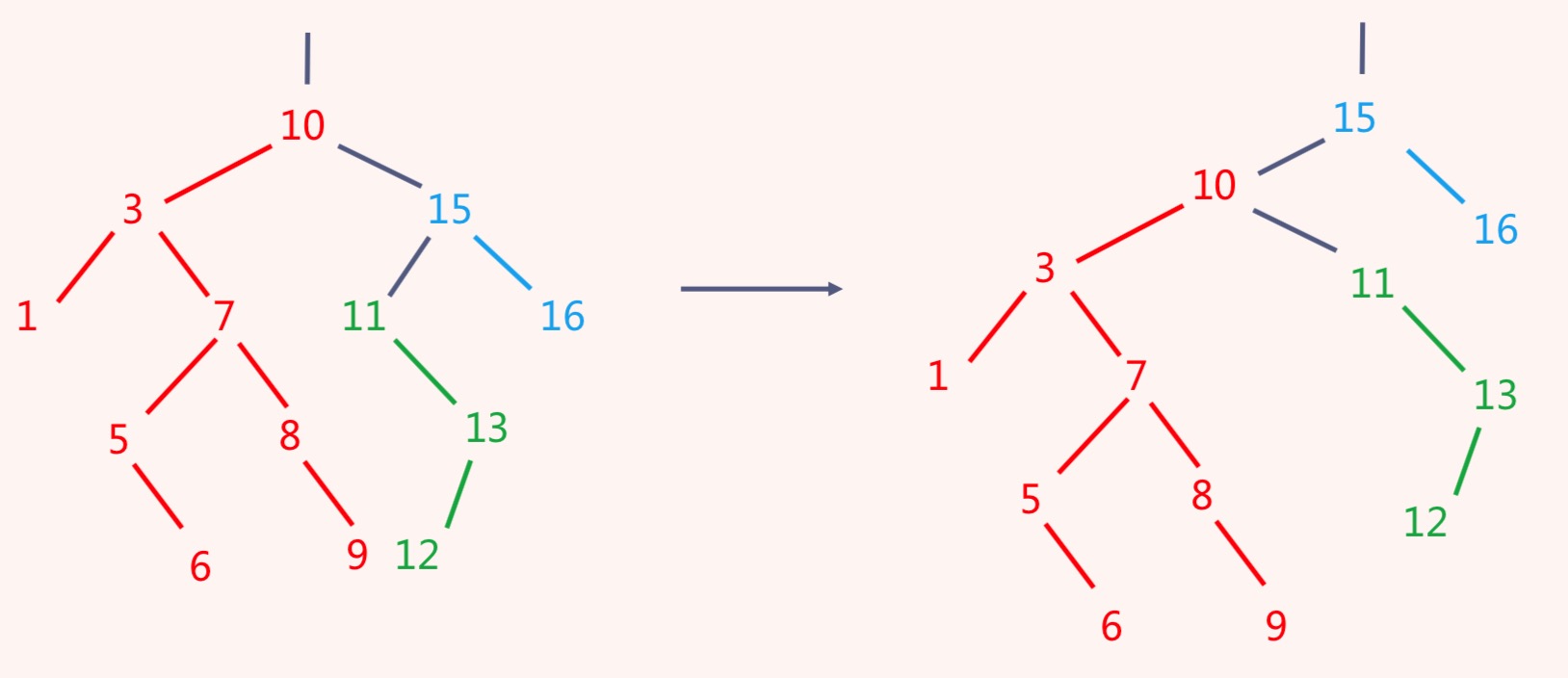
右旋：

第一次连边，节点x的子节点成为x的父节点的左子节点

第二次连边，节点x成为节点x的父节点的父节点的子节点，方向与x的父节点相同

第三次连边，节点x的父节点成为节点x的右子节点

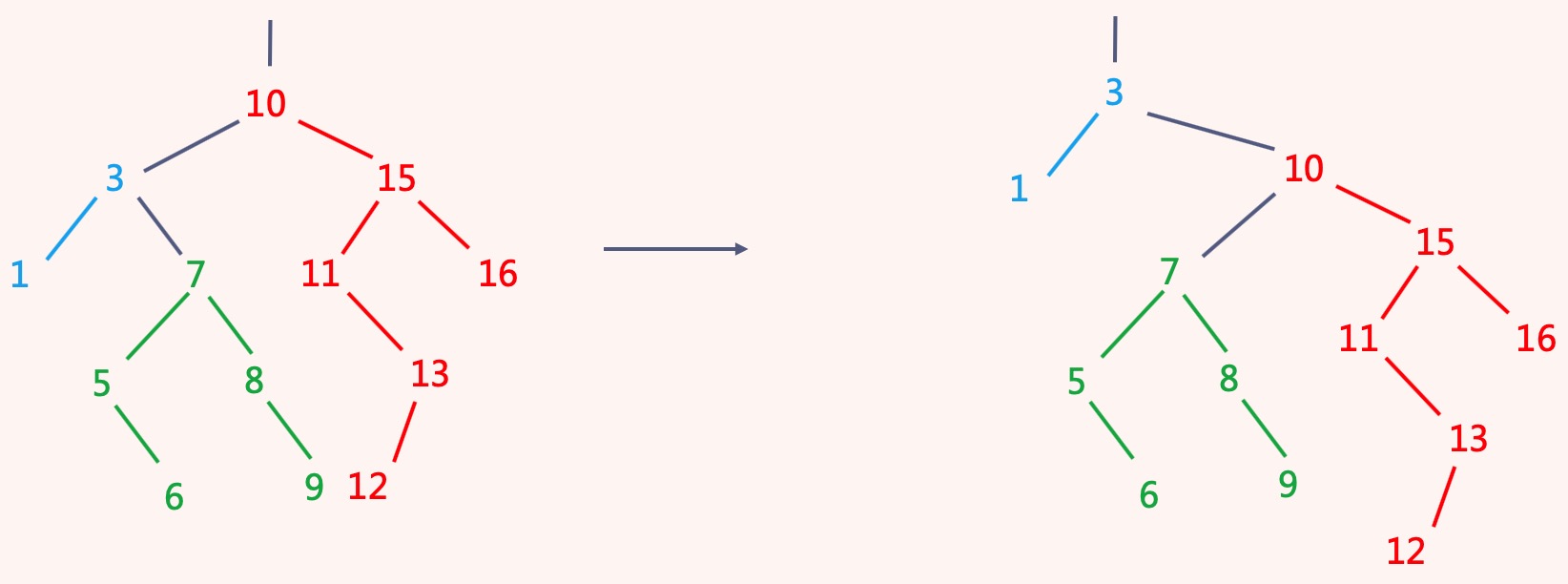
旋转操作只与标为红，蓝，绿的三个部分有关。

void rotate(int x) {
    int y = node[x].father, z = node[y].father, d = check(x), w = node[x].ch[d ^ 1]; //w判断应该左旋还是右旋
    connect(w, y, d); //第一次连边，节点x的子节点连接到x的父节点，方向与节点x相同
    connect(x, z, check(y)); //第二次连边，节点x连接到节点x的父节点的父节点，方向与x的父节点相同
    connect(y, x, d ^ 1); //第三次连边，节点x的父节点连接到节点x，方向与节点x原先的方向相反
    pushup(y); //更新子树
    pushup(x); //更新子树
}

伸展

splay

Splay操作：将节点x旋转到节点dist的子节点。通常是将该节点旋转到根节点，在这种情况下，应当将root置为x

最朴素的想法：只要父节点不是dist就一直旋转该节点，但这样很容易被某些机（wu）智（liang）出题人卡。

void splay(int x, int dist = 0) {
    while(node[x].father != dist) {
        rotate(x);
    }
    if(dist == 0) {
        root = x;
    }
}

所以，在实际操作中，通常会预判节点x的父节点的方向，若方向一致则旋转其父节点，减少被卡的可能性。

void splay(int x, int dist = 0) {
    for(int f = node[x].father; f = node[x].father, f != dist; rotate(x)) {
        if(node[f].father != dist) {
            if(check(x) == check(f)) {
                rotate(f); //方向一致则旋转x的父节点
            } else {
                rotate(x); //方向不一致则旋转x
            }
        }
    }
    if(dist == 0) {
        root = x;
    }
}

查找

find

查找值为x的节点，找到后将其置为root以便操作。

find操作的意义在于将值为x的节点伸展（splay）到根，在不存在值为x的节点的情况下，应将小于x的节点中最大的节点伸展（splay）到根。

void find(int x) {
    int cur = root;
    while(node[cur].ch[x > node[cur].v] != 0 && x != node[cur].v) {
        cur = node[cur].ch[x > node[cur].v]; //查找值为x的节点
    }
    splay(cur);
}

公共操作

如果将本文讲的Splay打包成一个class，则前文所述的操作应包含在private中，本节所述的操作应包含在public中。

insert

Splay中的insert其实与朴素BST中的insert没有什么区别，但若直接插入可能导致树退化为链，所以要在末尾处调用一次splay()函数，使Splay树保持平衡。

void insert(int x) {
    int cur = root, p = 0;
    while(cur != 0 && node[cur].v != x) {
        p = cur;
        cur = node[cur].ch[x < node[cur].v ? 0 : 1];
    }
    if(cur != 0) {
        node[cur].cnt++;
    } else {
        cur = ++cnt;
        if(p != 0) {
            node[p].ch[x <= node[p].v ? 0 : 1] = cur;
        }
        node[cur] = Node(x, p, 1, 1);
    }
    splay(cur);
}

serial

serial操作：查询值为x的节点，在find操作的基础上，serial只需要在find过后输出左子树节点数量即可。

int serial(int x) {
    find(x);
    return node[node[root].ch[0]].size
}

pre

找出值为x的节点的前驱，将节点splay到root后在左子树查找最大值即可。

int pre(int x) {
    find(x);
    if(node[root].v < x) {
        return root;
    }
    int cur = node[root].ch[0];
    while(node[cur].ch[1] != 0) {
        cur = node[cur].ch[1];
    }
    return cur;
}

suc

找出值为x的点的后继，与前驱同理。

int suc(int x) {
    find(x);
    if(node[root].v > x) {
        return root;
    }
    int cur = node[root].ch[1];
    while(node[cur].ch[0] != 0) {
        cur = node[cur].ch[0];
    }
    return cur;
}

remove

删除一个节点。

删除较为复杂，分四步来完成：

  1. 定义last为节点的前驱，next为节点的后继。
  2. 将last节点splay到root，这时last的左子树皆小于x
  3. 将next节点splay到last的子节右点，此时next的右子树皆大于x
  4. next的左节点rm必然满足 last < rm < next，删除rm即可
void remove(int x) {
    int last = pre(x), next = suc(x);
    splay(last);
    splay(next, last);
    int rm = node[next].ch[0];
    if(node[rm].cnt > 1) {
        node[rm].cnt--;
        splay(rm);
    } else {
        node[next].ch[0] = 0;
        pushup(next);
        pushup(root);
    }
}

rank

查找排名为k的节点

用一个指针cur从root开始查找，每次根据左子树大小于k的关系修改cur以及k。

int rank(int k) {
    int cur = root;
    while(1) {
        if(node[cur].ch[0] != 0 && k <= node[node[cur].ch[0]].size) {
            cur = node[cur].ch[0];
        } else if(k > node[node[cur].ch[0]].size + node[cur].cnt) {
            k -= node[node[cur].ch[0]].size + node[cur].cnt;
            cur = node[cur].ch[1];
        } else {
            return cur;
        }
    }
}

参考资料

伸展树- 维基百科，自由的百科全书

Splay Tree Introduction

版权声明：本博客所有文章除特别声明外，均采用 CC BY-NC-SA 许可协议。转载请注明出处！
本文链接：https://keepthethink.github.io/archives/1401793044/

Powered by Hexo
Theme - Material